Tangent to a Point outside of a circle
How to find the tangent to a point outside a circle
What You Start With
Shown above is a circle and a random point p that we are going to draw a tangent to
Tangent to a Point outside of a Circle
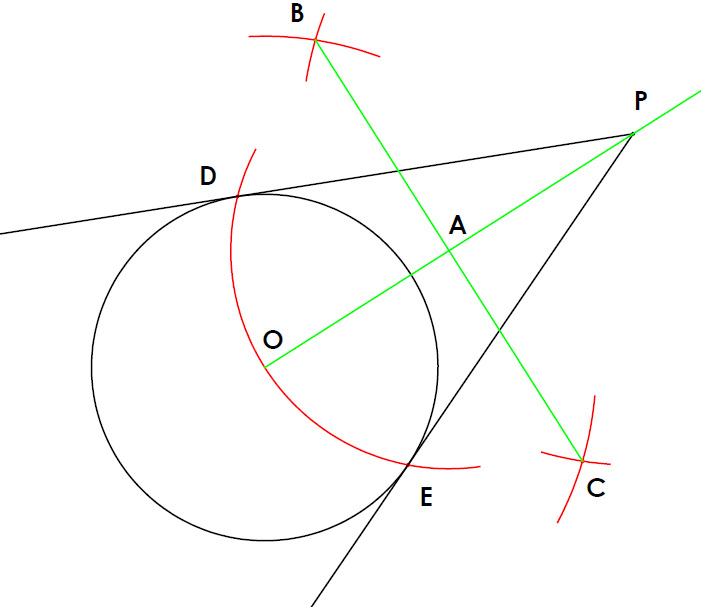
- The main thing to know before attempting this question is that the perpendicular bisector of a chord always passes through the centre of the circle. From this principle we can attempt to solve the question.
- First we join point P to the centre of the circle O and bisect this line. Depending on your position on point P this perpendicular bisector could be cutting your circle similar to a chord. (Go to the Interactive software at the bottom of the page to experiment with the position of point P)
- Where the perpendicular bisector, bisect line OP gives us point A. Take the radius AO and swing from point A. This circle will intersect the circle you were given at the start in two places. These two points are points of contact.
- Join point P through these two points to create two tangents. Any point outside a circle will always have two possible tangents to that circle.
Tangent to a Point on a Circle Interactive
- Move the centre point of the circle to change the position of the centre point of the circle.
- Move Point P to change the position of point P
- Notice how you always have two tangents to the circle from point P until you place the point P on the circle or inside it.