Tangent to a Point on the Circle
How to construct a tangent to a point on a circle
What You Start With
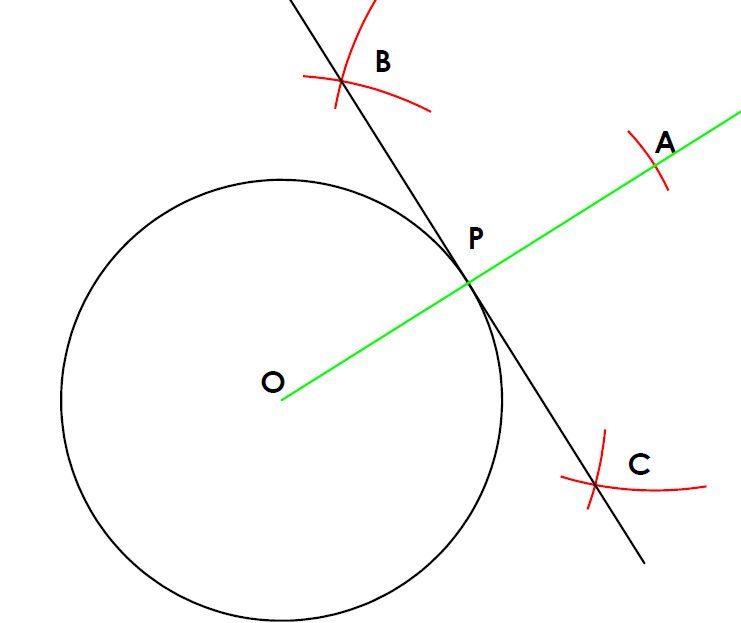
Shown above is a circle with a random point P selected.
Tangent to a Point on a circle
- The main principle we are going to solve this question with is that the a tangent to a circle is perpendicular to a line drawn from the center of a circle to the point of contact.
- With that in mind we start by joining the center to point P and extending it on. We know that the tangent will be perpendicular to this line, so what we do is take distance OP on our compass and swing from point P and where it cuts the line you previously drew will create point A.
- Next we are going to bisect line OA and the resulting bisector will be a tangent at point P because we know that distance OP and distance PA are equal since they were drawn with the same radius.
Tangent to a Point on a Circle Interactive
- Move point A to change the position of the center point of the circle.
- Move Point P to change the position of point P and also the radius of the circle.
- Notice how the line drawn from the center of the circle to the point of contact will always remain 90 degrees to the tangent.