Constructing A Circle given three points
How to draw a circle having just three point that are on that circle
What You Start With
Shown above is three random points that we are going to try and place a circle on.
Constructing a Circle given three points
- The main thing to know before attempting this question is that the perpendicular bisector of a chord always passes through the centre of the circle. From this principle we are going to find and draw the circle.
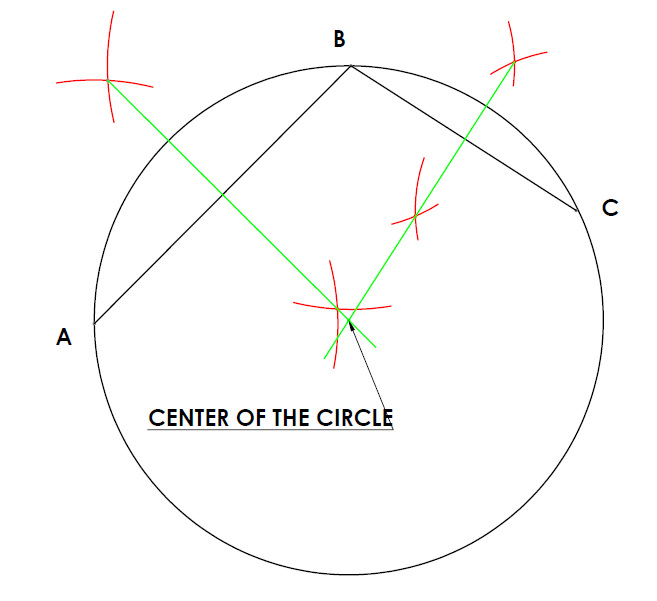
- Start by drawing two lines between the three points given. I joint point A to B and Point B to C. (You can also join point A to C. It will still work)
- Next bisect these two lines you have just drawn and extend the bisector if necessary. Where these two bisectors (shown above in green) intersect gives us the the centre point of the circle.
- Finally get your compass and swing a radius from the centre point to any of the three points. Your subsequent circle will pass through point A, B and C as required.
Proving that the bisectors of the three chords you could create will intersect at the centre point
- Drag Points A, B and C to change the points positions.
- Notice how the circle changes size and that the bisectors of all three chords still intersect at the centre point regardless of where the points are placed.