Perpendicular from a Line to an External Point
How to draw a perpendicular from an external point to a line
What you start with
Shown above is a line of any length and a point P. Point P can be below the line also.
The Theory Behind How It Works
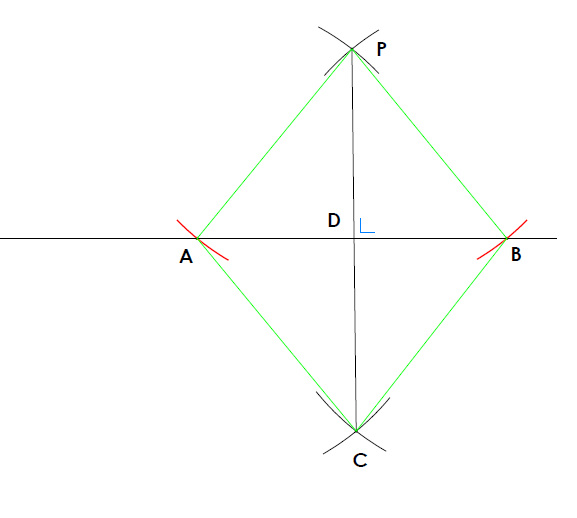
Proof:
Q.E.D.
- Line PA is congruent with line PB because they were both drawn with the same compass radius. The compass radius isn't specific but it must be able to cut the line in two places, so ensure the radius is big enough.
- Line CA is congruent with line CB because they were both drawn with the same compass radius.
- Triangle ∆PAC and ∆PBC are congruent they have 3 sides congruent. PC is common to both. We proved in step 1 and 2, that PA and PB were congruent while also CA and CB are congruent.
- Angle DPA and DPB are congruent because corresponding parts of congruent triangles are congruent. (The angles with the black dots)
- Triangle ∆DPA and DPB are congruent because two sides are congruent (PA and PB are congruent and PD is common to both triangles) and they have an angle in common (see Step 4)
- Angle PDA and PDB are congruent because corresponding parts of congruent triangles are congruent. Also since they are supplementary and congruent angles they must be 90°. Therefore line DP is perpendicular to the given line as required.
Q.E.D.