Circles
A Circle is a plane figure similar to a triangle. A plane figure is a flat figure (2D shape). This means that it has a height and a length but no thickness. A circle is the path of a point which is a set distance away from a given point called the centre. There are numerous everyday examples of circles in both nature and design. Coins, sign posts and some logos are just a few.
Circles are constructed using a compass. The metal point of the compass is placed on the centre of the circle and is not removed until the circle is drawn. The compass is then rotated about this point. While Rotating you ensure that the lead point of the compass is in contact with the paper.
In this section we will go into an in-depth look at circles and answer a few question at the end.
Click on the links below to get transferred to whatever information or construction you want to.
Circles are constructed using a compass. The metal point of the compass is placed on the centre of the circle and is not removed until the circle is drawn. The compass is then rotated about this point. While Rotating you ensure that the lead point of the compass is in contact with the paper.
In this section we will go into an in-depth look at circles and answer a few question at the end.
Click on the links below to get transferred to whatever information or construction you want to.
|
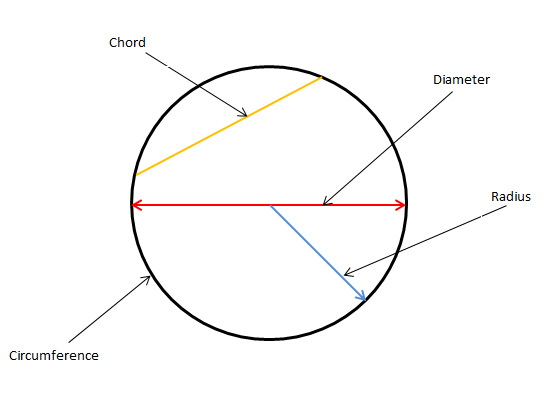
Parts of a Circle - In this section we will go through all the parts of a circle in detail.
. |
|
Eccentric/Concentric Circles - In this section we will distinguish the difference between concentric and eccentric circles. We also learn the properties of each.
|
Circle Proofs
There is a couple of things that will never change regardless of what size circle you use but it is still important to know how to prove them and understand why they never change. In Mathematics these proofs on circles can be examined. For more information on these proofs click on the link below.
Questions
At this stage we have covered all the basic information we need to construct circles so if you are confident on all the information covered up until this stage it is time to attempt a few questions. These questions will also incorporate information we learned in all the previous sections of this website.
Tangents to Circles
If you have completed all the above sections and understand it, the final thing to learnon circles is about tangents to circles. A tangent, is a line that hits a circle only at one exact point. This point is called the point of contact. For more information on tangent to circles and some questions click on the link below.