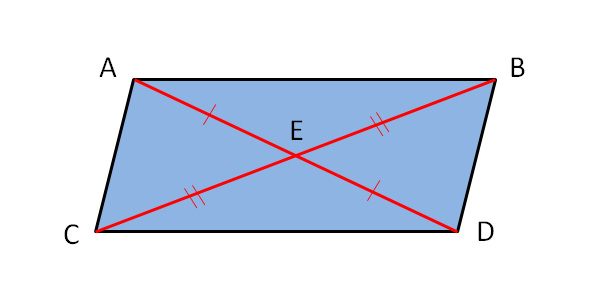
Proving the Diagonals of a Parallelogram bisect each other
How to prove the diagonals of a parallelogram bisect each other into equal length.
Proof:
Therefore the diagonals of a parallelogram do bisect each other into equal parts.
- Given above is Quadrilateral ABCD and we want to prove the diagonals bisects each other into equal lengths.
- First we join the diagonals and where they intersect is point E.
- Angle ECD and EBA are equal in measure because lines CD and AB are parallel and that makes them alternate angles.
- Angles EDC and EAB are equal in measure for the same reason.
- Line CD and AB are equal in length because opposite sides in a parallelogram are are equal.
- Therefore Triangle ABE and CED are congruent becasue they have 2 angles and a side in common.
- Hence line CE and EB are equal and AE and ED are equal due to congruent triangles.
Therefore the diagonals of a parallelogram do bisect each other into equal parts.
Interactive of Proof