Constructing A Triangle containing 30, 60, 90 degrees given the hypotenuse (without using set squares)
How to construct a Triangle containing 30°, 60° and 90°, given the hypotenuse
The theory behind how it works
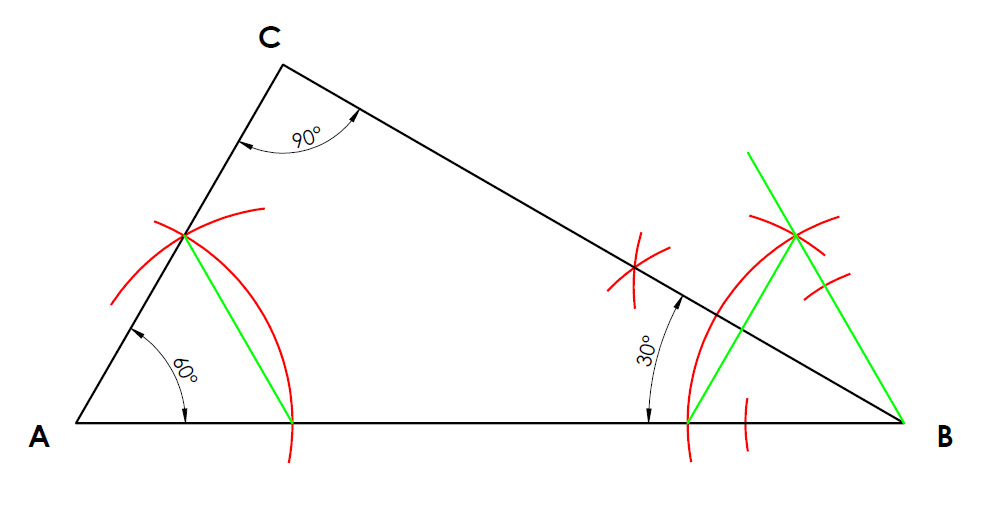
Construction 1
Constructing an A triangle containing 30, 60, 90 degrees given the hypotenuse.
- Since we are constructing a right angled triangle we know that the hypotenuse is always opposite the 90 degree angle.
- We draw the hypotenuse (Line AB)
- Next we construct a 60 angle at point A. (It does not necessarily have to be from point A it can just as easily be from point B.) If you are unsure of this step go to the Constructing a 60 degree line.
- From the other end point of the hypotenuse we construct a 30 degree, simply by drawing a 60 degree line first and then bisecting the angle. see constucting a 30 degree line if you are unsure.
- Finally extend on the 60 and 30 degree lines that you are just after constructing and where they meet will automatically make a 90 degree line. 60 + 30 + 90 = 180 degrees.
- Therefore the construction is completed as required. the triangle contains a 30, 60, and 90 degree angle with the required hypotenuse.
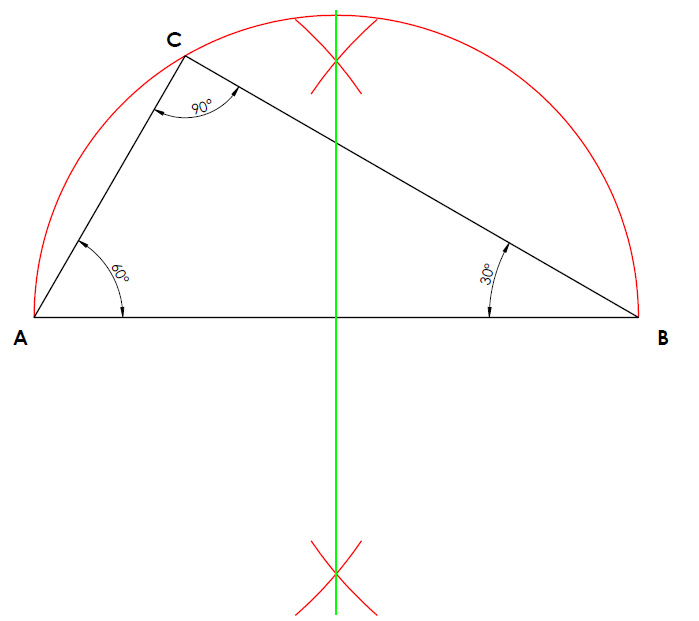
Construction 2
Constructing an A triangle containing 30, 60, 90 degrees given the hypotenuse.
Note:
- Since we are constructing a right angled triangle we know that any triangle constructed using the diameter and containing a point on the circumference is going to be a right angled triangle.
- We start off by drawing the hypotenuse of the given length and then bisecting it, giving us the midpoint. Construct a semi circle having line AB as the diameter.
- Next you could use your protractor and construct an angle of 60 degree from point A. Where this angle meets the semi circle gives you a new point C. Join point C back to point A to complete your triangle of 30, 60, 90 degrees.
Note:
- If you are told to show all constructions in the question (meaning you cannot use a protractor) then you simply construct a 60 degree line using you compass and straightedge.
Proof that if you draw a triangle inside a semi circle, the angle opposite the diameter is 90 degrees
- Drag point C to show that the angle will always remain 90 degrees.
- Move Point A or B to see no matter how big the diameter or angle the diameter is at, the angle opposite will still be 90 degrees.