Constructing a Triangle with a given perimeter in the ratio 2:3:4
How to construct a triangle given the perimeter in the ratio 2:3:4
The theory behind how it works
Constructing a triangle from a given perimeter in the ratio of 2:3:4
- In order to get the perimeter in the ratio of 2:3:4 we add them together to get 9.
- We now know that we will have to divide the perimeter into 9 equal parts using the dividing a line into an equal amount of parts principle.
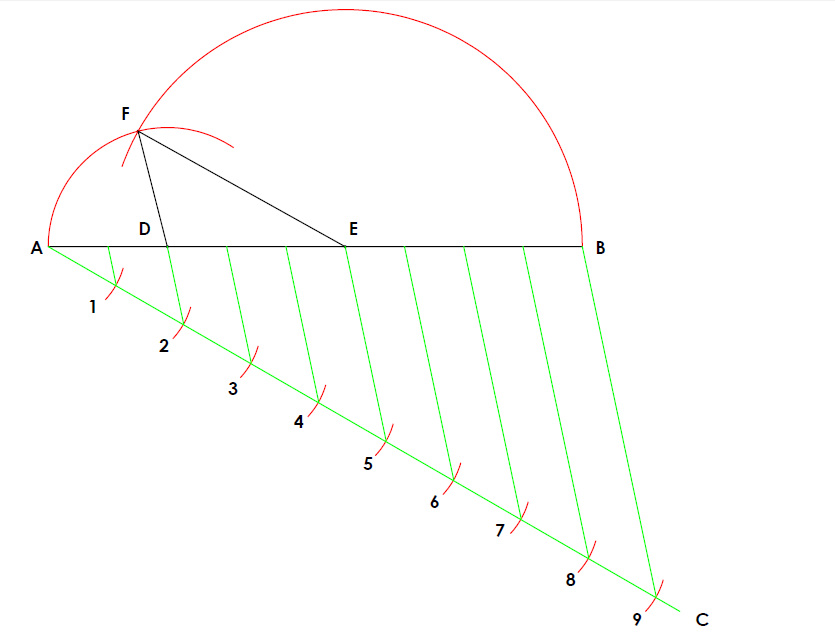
- Draw a line at any angle from Point A or B (it doesn't matter which one choose) any length, represented by the green line above.
- Mark off nine steps with your compass, using the same radius.
- Join the ninth arc back to point B.
- Bring the rest of the arcs back parallel to the line B9. Where these lines meet the perimeter line we drew at the start give us nine new points. I moved two spaces over from point A and called it point D. I also moved 4 spaces from point B and called that point E. Notice how their is 3 spaces left between point D and E.
- Next i swung an arc of radius AD from point D and an arc of radius EB from point E. Where the two arcs intersect create point F. Finally we join point D to F and point E to F, creating a triangle in the ratio of 2:3:4 of the given perimeter.